定义
感知器是激活函数为阶跃函数的神经元。感知器的模型如下: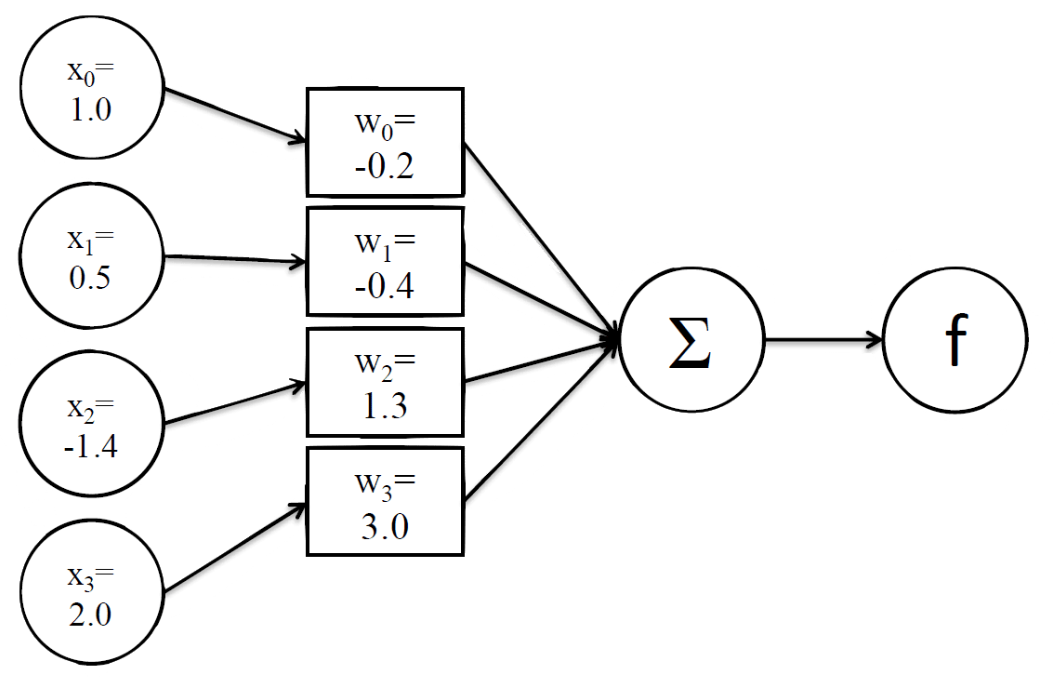
· 输入(inputs):一个感知器可以接收多个输入(x1,x2,…,xn|xi∈R)
· 权值(weights):每一个输入上都有一个权值wi∈R,此外还有一个偏置项b∈R,也就是上图的w0。
· 加权和(weighted sum):就是输入权值 x x 权值 w + 偏置项 b的总和。
· 激活函数(step function):感知器的激活函数:
· 输出(output):感知器的输出由加权值用激活函数做非线性变换。也就是这个公式:y=f(w⋅x+b)
我们使用unit激活函数结合上图就有:
y=f(w⋅x+b)=f(w1x1+w2x2+w3x3+bias)
其中f(x)就是激活函数 f(x)={1x>0 0x≤0 ,图像如下图所示: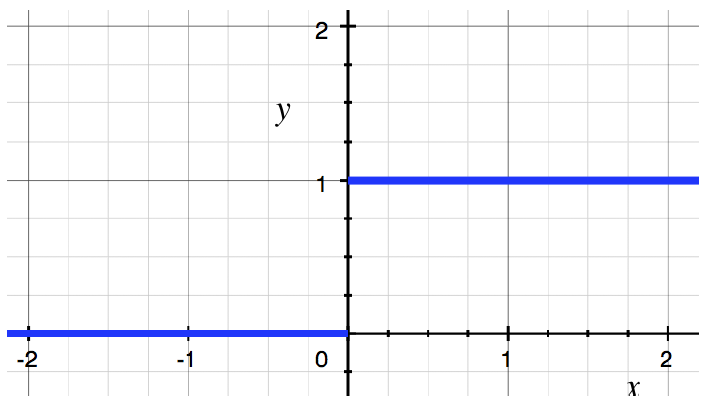
实例
则:
所以:
带入激活函数:
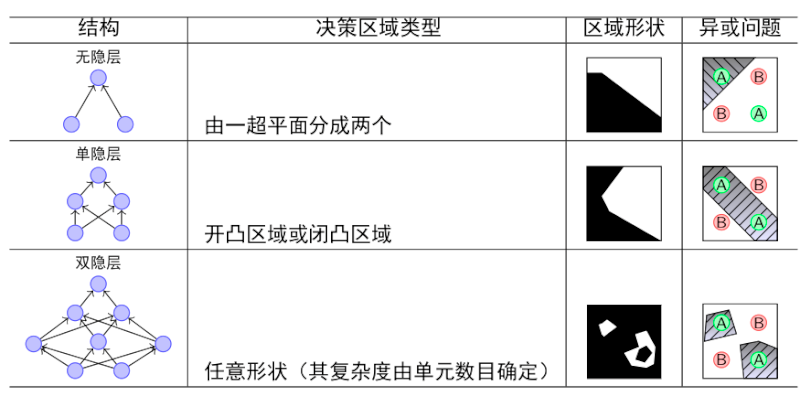
隐层
激活函数
unit激活函数:

sigmod激活函数:
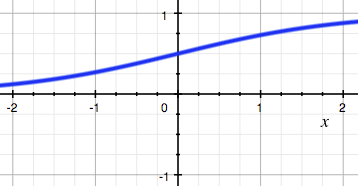
tanh激活函数:
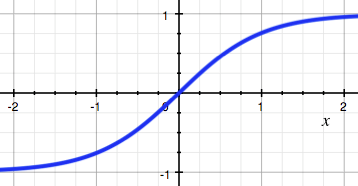
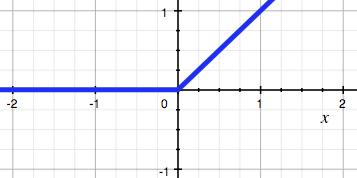
relu激活函数:
激活函数的作用
引入非线性因素。
在我们面对线性可分的数据集的时候,简单的用线性分类器即可解决分类问题。但是现实生活中的数据往往不是线性可分的,面对这样的数据,一般有两个方法:引入非线性函数、线性变换。
线性变换
就是把当前特征空间通过一定的线性映射转换到另一个空间,让数据能够更好的被分类
激活函数的特点
unit:线性分界– 几乎已经不用了
sigmoid:非线性分界– 两端软饱和,输出为 (0,1)区间
– 两端有梯度消失问题
– 因为输出恒正,可能有 zig现象
tanh:非线性分界 :非线性分界– 两端软饱和,输出为 (-1, 1) 区间
– 仍然存在梯度消失问题
– 没有 zig,收敛更快 (LeCun 1989)
ReLU:非线性分界 – 左侧硬饱和,右无输出为 [0,+∞)区间– 左侧会出现梯度一直为 0的情况,导致神经元 不再更新(死亡)
– 改善了梯度弥散
– 同样存在 zig