ε-贪婪(greedy)策略
目的:探索与利用
ε∈(0,1),随着时间的推移逐渐减小直至0
产生一个(0,1)的随机数m
如果ε>m
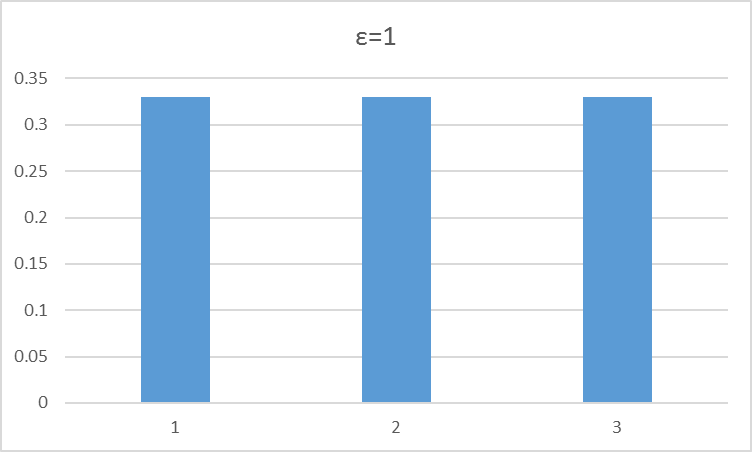
采取随机策略,例如一共4个动作,那么选每一个动作的概率都是 0.25
如果ε<m
采取贪婪策略,计算当前网络所有输出值Q(St,a),选择使得 Q(St,a)最大的那个at值作为下一步的动作
玻尔兹曼softmax
$q_t(a)$为t时刻,采取动作a的Q值大小
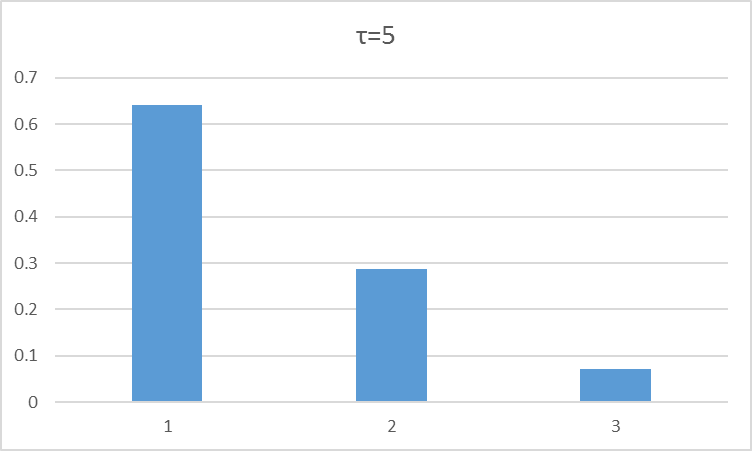
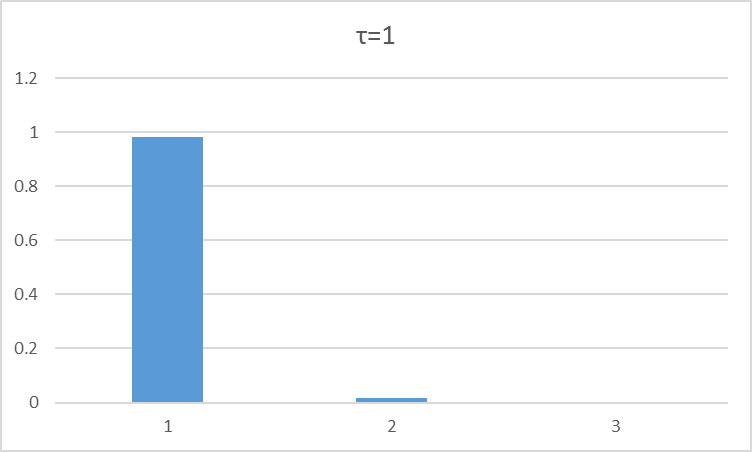
τ表示是一个衰减系数(类似于模拟退火算法的温度项),随着训练次数的增加而逐渐减少,与ε相对应。
随着τ的减小,选择使Q值最大的那个动作a值的概率也越来越高。
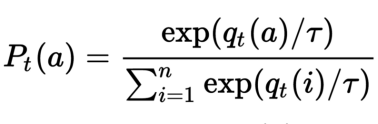
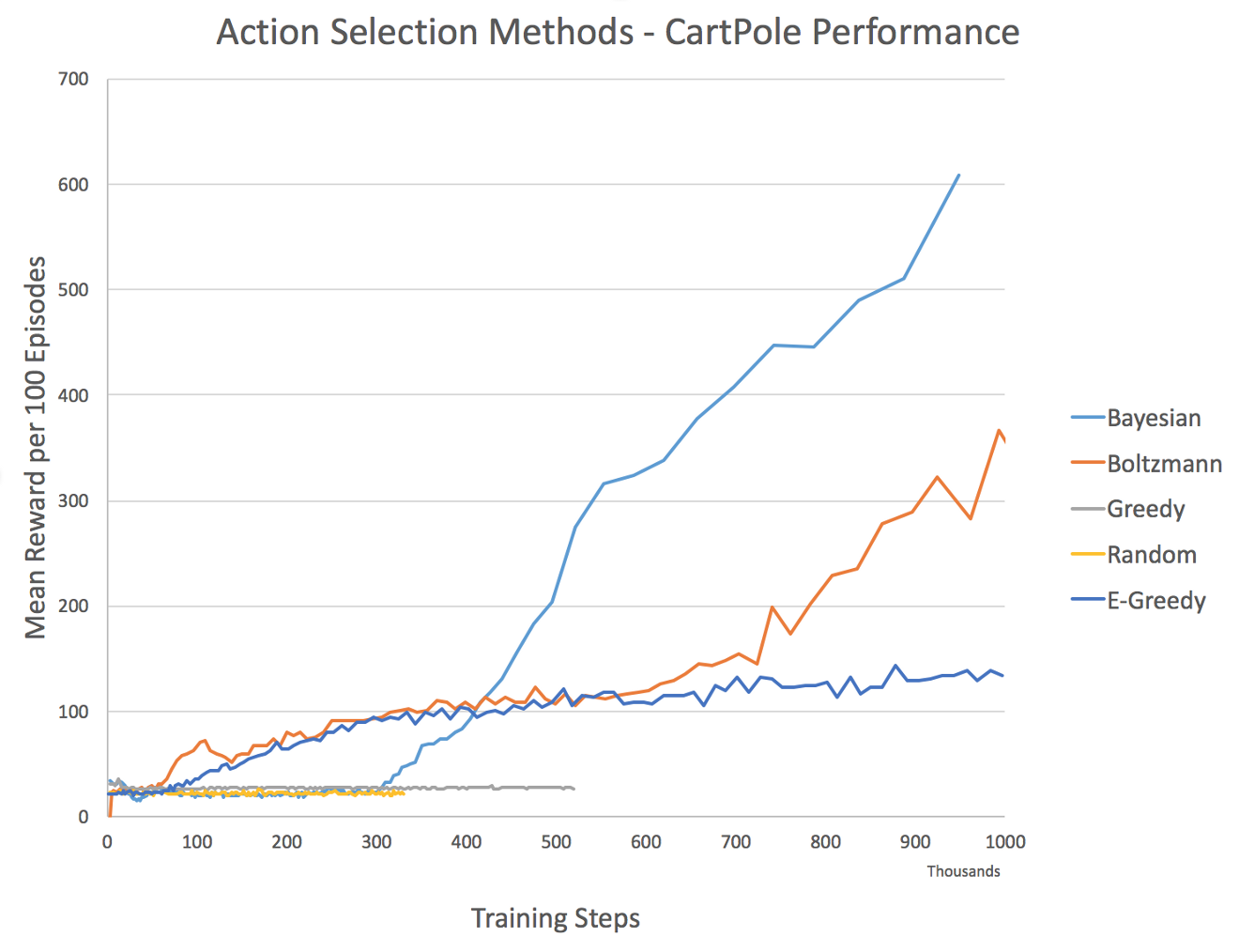
ε-贪婪 VS 玻尔兹曼
`

DDQN
DQN:

Double Q learning:
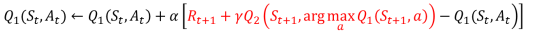
Double DQN:
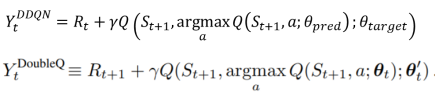
PRIORITIZED EXPERIENCE REPLAY(优先化记忆回放)
每一个rollout的被采样概率:
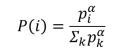
其中:
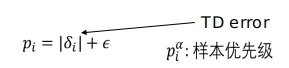
importance-sampling (IS) weights(重要性采样权重):
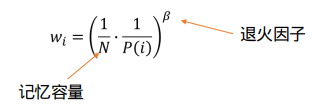
SumTree:
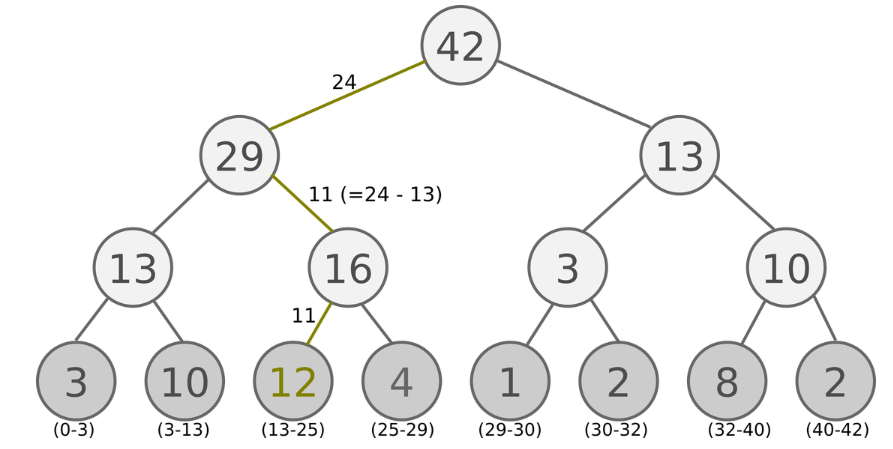
DDQN+PER:

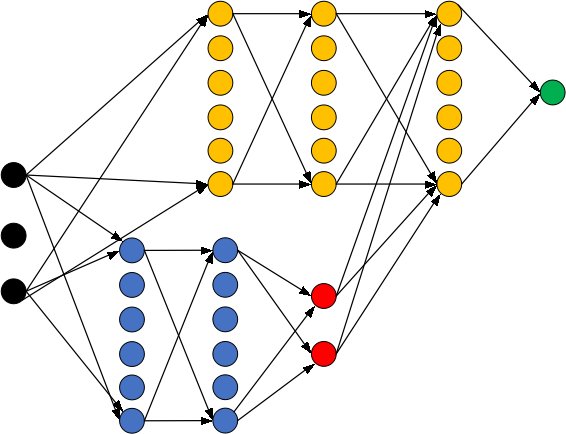
Dueling DQN
Dueling Network Architectures for Deep Reinforcement Learning
value和Q value:
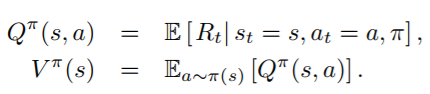
优势值(Advantage function)
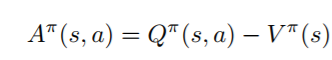
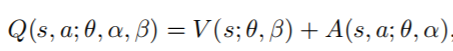
结合方式:
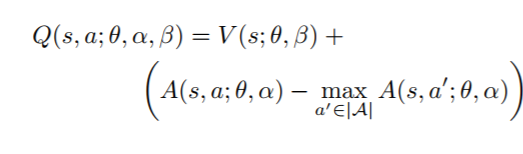
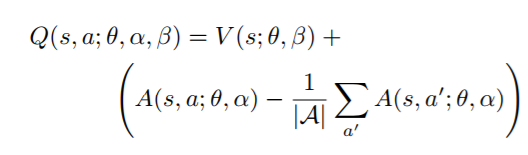
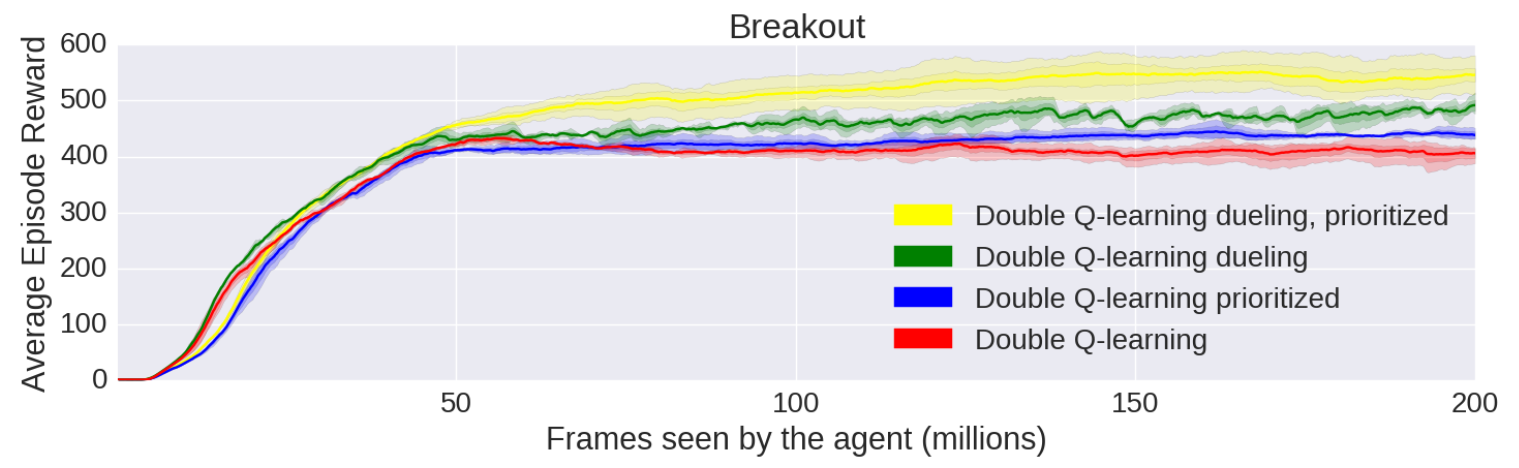
DQN性能
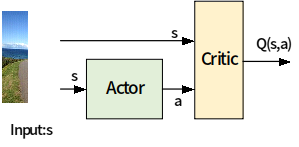
DDPG
DQN的问题:
动作空间必须是离散的
能不能将DQN的思想应用到连续的动作空间?
DDPG 是一种离策略算法
DDPG仅可以用于连续动作空间的问题