循环神经网络(RNN)是一类神经网络,包括一层内的加权连接,与传统前馈神经网络相比,加权连接仅反馈到后续层。因为RNN包含循环,所以RNN就可以在处理输入信息的时候同时储存信息。这种记忆使得RNN非常适合处理必须考虑事先输入的任务(比如时序数据)。所以循环神经网络在自然语言处理领域非常适合。
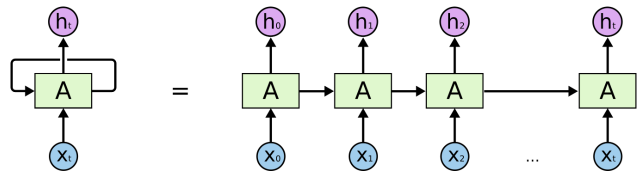
传统神经网络(包含CNN),输入和输出都是互相独立的。
RNN引入了“记忆”的概念
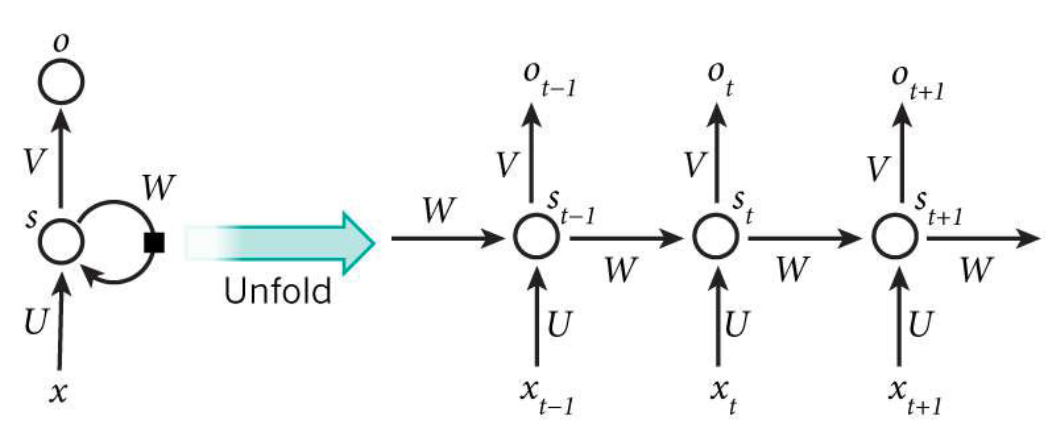
x:输入层的值
U:输入层到隐层的权重参数
s:隐层的值
v:隐层到输出层的权重参数
o:输出层的值
W:递归神经网络的隐藏层的值s不仅仅取决于当前这次的输入x,还取决于上一次隐藏层的值s。权重参数W就是隐藏层上一次的值作为这一次的输入的权重。
关键点:$St$的值不仅仅取决于$X_t$,还取决于$S{t−1}$(就是上一状态的隐层的值)
循环神经网络的计算公式:
输出层的计算公式,由于输出层是一个全连接层,所以说它每个节点都和隐层的节点相连。V是输出层的权重参数,f是激活函数。
隐层的计算公式,它是一个循环层,U是输入x的权重参数,W是上一次的值$S_{t−1}$作为这一次输入的权重参数,f是激活函数。
总结:从上面的公式中,我们可以看出,循环层和全连接层的区别就是循环层多了一个权重参数w。
扩展:如果反复的把(1)式带入 (2)式:
${O}_t=f(V\cdot{S}_t)$
`
`
`
`
总结:从上面可以看出,递归神经网络的输出值$ot$,是受前面几次输入值$X_t、X{t−1}、X{t−2}、X{t−3}…$影响的,这也就是为什么递归神经网络可以往前看任意多个输入值的原因。
双向递归神经网络
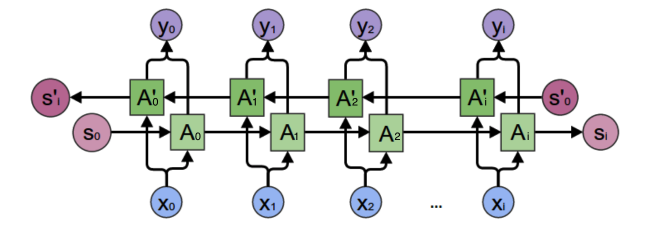
从上图可以看出,双向递归神经网络的隐层是需要保持两个值:
- A:参与正向计算
- A′:参与反向计算
所以$y_2$的值就取决于$A_2$和$A′_2$。计算方法:
$A_2和A_2′$则分别计算:
总结:
- 正向计算时:隐层的值有关。
- 反向计算时:隐层的值有关。
- 最终的输出取决于正向和反向计算的和。
扩展:我们仿照(1)和(2)那种方式:
注意:从上面三个公式我们可以看到,正向计算和反向计算不共享权重,也就是说U和U’、W和W’、V和V’都是不同的权重矩阵。
深度递归神经网络
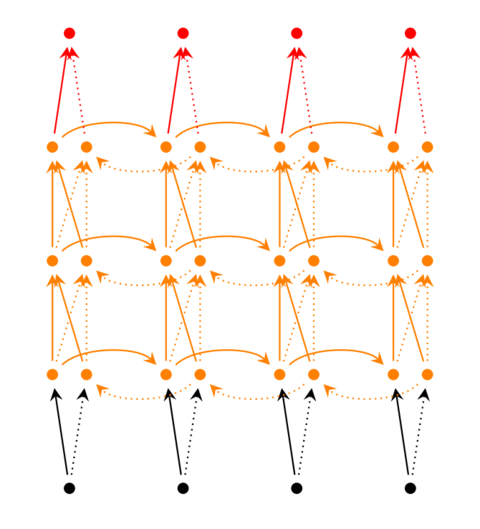
我们把第ii个隐层的值表示为$S_t^{(i)}、S_t’^{(i)}$ ,则深度递归神经网络的计算方式就可以表示为:
总结
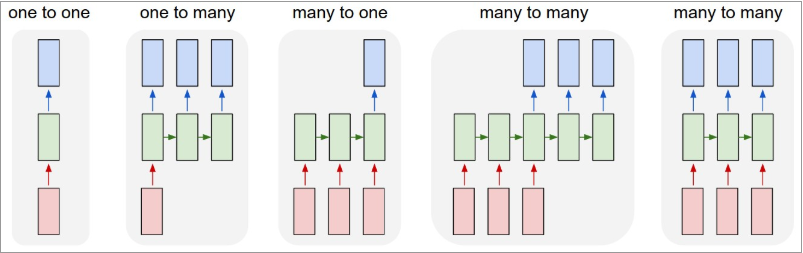
从上图我们可以总结出:
one to one:一个输入(单一标签)对应一个输出(单一标签)one to many:一个输入对应多个输出,即这个架构多用于图片的对象识别,即输入一个图片,输出一个文本序列。many to one: 多个输入对应一个输出,多用于文本分类或视频分类,即输入一段文本或视频片段,输出类别。many to many:这种结构广泛的用于机器翻译,输入一个文本,输出另一种语言的文本。many to many:这种广泛的用于序列标注。
在众多的深度学习网络中,RNN由于能够接收序列输入,也能得到序列输出,在自然语言处理中取得了巨大的成功,并得到广泛的应用。