梯度下降

梯度下降方法

用负梯度作搜索方向，即令$\bigtriangleup x=-\bigtriangledown f(x)$, 是一种自然的选择。相应的方法就称梯度方法或者梯度下降方法。

梯度下降算法的概念

梯度下降算法是一个被广泛使用的优化算法, 它可以用于寻找最小化成本函数的参数值. 也就是说: 当函数$ J(\theta)$取得最小值时, 求所对应的自变量θ的过程， 此处θ就是机器要学习的参数，$J(\theta)$就是用于参数估计的成本函数, 是关于θ的函数.

梯度下降的基本步骤

梯度下降法的计算过程就是沿梯度下降的方向求解极小值（也可以沿梯度上升方向求解极大值）

给定 初始点:$x \in dom f$

重复进行：

1. $\bigtriangleup x :=-\bigtriangledown f(x)$
2. 直线搜索。通过精确或回溯直线搜索方法确实步长t.
3. 修改 :$x =x+t\bigtriangleup x$

直到：满足停止准则。

换种方式：

1. 对成本函数进行微分, 得到其在给定点的梯度. 梯度的正负指示了成本函数值的上升或下降:$Δ(\theta)=\frac{∂J(\theta)}{∂\theta}$
2. 选择使成本函数值减小的方向, 即梯度负方向, 乘以学习率为 α 计算得参数的更新量, 并更新参数:$\theta=\theta−αΔ(\theta)$
3. 重复以上步骤, 直到取得最小的成本

批量梯度下降法（Batch Gradient Descent）

　批量梯度下降法，是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来进行更新，这个方法对应于线性回归的梯度下降算法，也就是说线性回归的梯度下降算法就是批量梯度下降法。

具体实现过程：

---

1. 假设函数:$h_\theta = \sum_{i=1}^n\theta_ix_i$
2. 成本函数:$J(\theta)=\frac{1}{2m} \sum_{i=1}^n(h_\theta(x_i)-y_i)^2$
3. 对成本函数进行求偏导：对每一个参数$\theta_j$进行分别求偏导，得出各自的梯度。$\frac{\partial J(\theta)}{\partial \theta}=-\frac1 m \sum_{i=1}^n(y_i-h_\theta(x_i))x_j^i$
4. 每个参数都按照梯度的负方向进行更新:

$$\theta_j=\theta_j+\frac a m \sum_{i=1}^n(y_i-h_\theta(x_i))x_j^i$$

---

BGD伪代码：

---

repeat{

$$\theta_j=\theta_j+\frac a m \sum_{i=1}^n(y_i-h_\theta(x_i))x_j^i$$

(for every j = 0, 1, .. n)

}

---

总结：

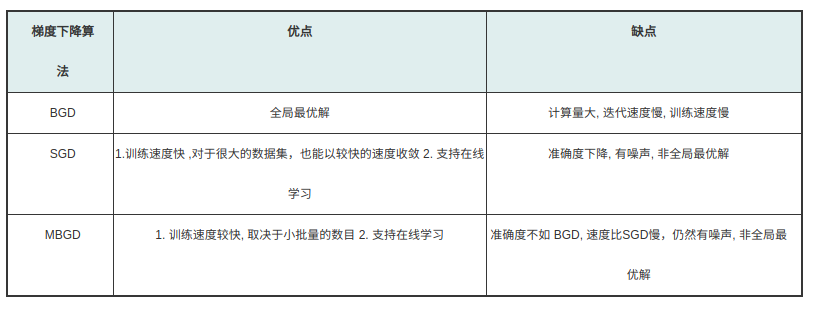
优点：BGD 得到的是全局最优解, 因为它总是以整个训练集来计算梯度,

缺点：因此带来了巨大的计算量, 计算迭代速度很很慢.

随机梯度下降法（Stochastic Gradient Descent）

随机梯度下降法，其实和批量梯度下降法原理类似，区别在于求梯度时没有用所有的m个样本的数据，而是仅仅选取一个样本j来求梯度。

具体实现过程：

SGD 每次以一个样本, 而不是整个数据集来计算梯度. 因此, SGD 从成本函数开始, 就不必再求和了, 针对单个样例的成本函数可以写成:

$$J(\theta)=\frac{1}{2} (h_\theta(x_i)-y_i)^2$$

于是, SGD 的参数更新规则就可以写成 ：

$$\theta_j=\theta_j+a (y_i-h_\theta(x_i))x_j^i$$

SGD伪代码：

---

repeat {     

for i = 1, .., m{    

$$\theta_j=\theta_j+a (y_i-h_\theta(x_i))x_j^i$$

        (for every j = 0, 1, .. n)    

}

}

---

总结：

SGD 的关键点在于以随机顺序选取样本. 因为 SGD 存在局部最优困境, 若每次都以相同的顺序选取样本, 其有很大的可能会在相同的地方陷入局部最优解困境, 或者收敛减缓. 因此, 欲使 SGD 发挥更好的效果, 应充分利用随机化带来的优势: 可以在每次迭代之前 (伪代码中最外围循环), 对训练集进行随机排列.

缺点：因为每次只取一个样本来进行梯度下降, SGD 的训练速度很快, 但会引入噪声, 使准确度下降

优点：可以使用在线学习. 也就是说, 在模型训练好之后, 只要有新的数据到来, 模型都可以利用新的数据进行再学习, 更新参数,以适应新的变化.

ＢＧＤ vs ＳＧＤ

随机梯度下降法和批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

MBGD就综合了这两种方法的优点。

小批量梯度下降法（Mini-batch Gradient Descent）

MBGD 是为解决 BGD 与 SGD 各自缺点而发明的折中算法, 或者说它利用了 BGD 和 SGD 各自优点. 其基本思想是: 每次更新参数时, 使用 n 个样本, 既不是全部, 也不是 1. (SGD 可以看成是 n=1 的 MBGD 的一个特例)

MBGD 的成本函数或其求导公式或参数更新规则公式基本同 BGD 。

MBGD 的伪代码：

---

say b=10, m=1000,

repeat {     

for i = 1, 11, 21, .., 991 {

$$\theta_j=\theta_j+\frac a {10} \sum_{i=1}^{i+9}(y_i-h_\theta(x_i))x_j^i$$

 (for every j = 0, 1, .. n)    

 }

}

---

梯度下降算法总结