GAN理论

简介

对抗神经网络其实是两个网络的组合，可以理解为一个网络生成模拟数据，另一个网络判断生成的数据是真实的还是模拟的。生成模拟数据的网络要不断优化自己让判别的网络判断不出来，判别的网络也要优化自己让自己判断得更准确。二者关系形成对抗，因此叫对抗生成神经网络。

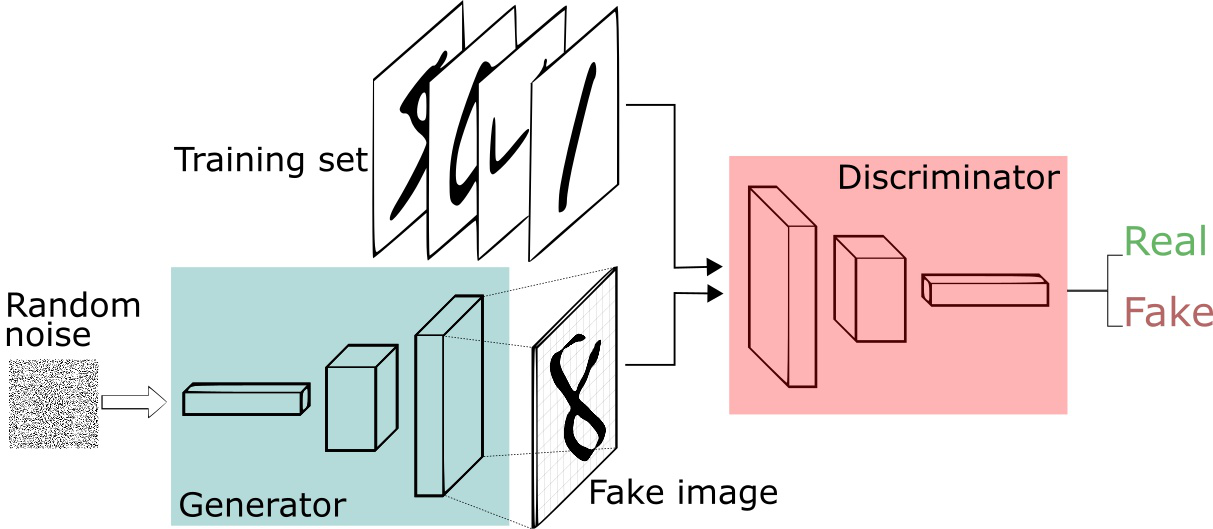
GAN由generator（生成式模型）和discriminator（判别式模型）两部分构成。

$\bullet$ generator：主要是从训练数据中产生相同分布的samples，对于输入x，类别标签y，在生成式模型中估计其联合概率分布（两个及以上随机变量组成的随机向量的概率分布）。

$\bullet$ discriminator：判断输入是真实数据还是generator生成的数据，即估计样本属于某类的条件概率分布。它采用传统的监督学习的方法。　

基本结构

生成器

生成式模型又叫生成器。它先用一个随机编码向量来输出一个模拟样本。

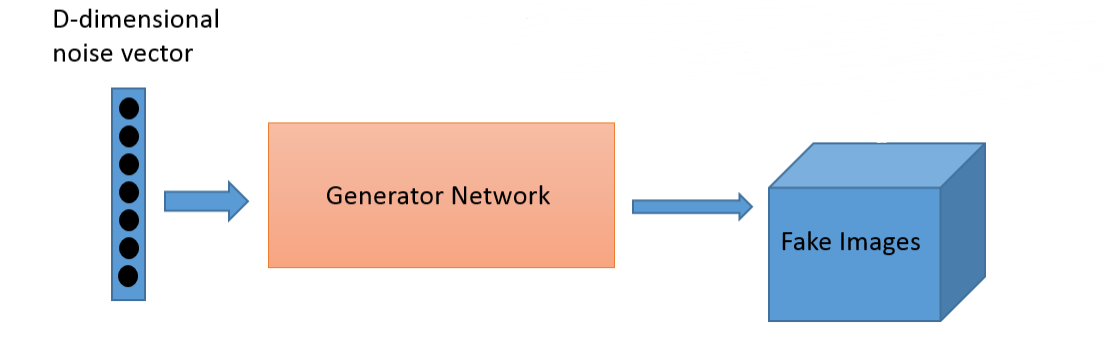
一般的生成模型, 必须先初始化一个“假设分布”，即后验分布， 通过各种抽样方法抽样这个后验分布，就能知道这个分布与真实分布之间究竟有多大差异。这里的差异就要通过构造损失函数(loss function)来估算。

判别器

判别式模型又叫判别器。它的输入是一个样本（可以是真实样本也可以是模拟样本），输出一个判断该样本是真样本还是模拟样本（假样本）的结果

总结：判别器的目标是区分真假样本，生成器的目标是让判别器区分不出真假样本，两者目标相反，存在对抗。

我们可以把生成模型看作一个伪装者，而把判别模型看成一个警察。生成模型通过不断地学习来提高自己的伪装能力，从而使得生成出来的数据能够更好地“欺骗”判别模型。而判别模型则通过不断的训练来提高自己的判别能力，能够更准确地判断出数据的来源。GAN就是这样一个不断对抗的网络。

$\bullet$ 生成模型以随机变量作为输入，其输出是对真实数据分布的一个估计。
$\bullet$ 生成数据和真实数据的采样都由判别模型进行判别，并给出真假性的判断和当前的损失。
$\bullet$ 利用反向传播，GAN对生成模型和判别模型进行交替优化。

例子

假设数据的概率分布为M，但是我们不知道具体的分布和构造是什么样的，就好像是一个黑盒子。为了了解这个黑盒子，我们就可以构建一个对抗生成网络：

$\bullet$　生成模型G：使用一种我们完全知道的概率分布N来不断学习成为我们不知道的概率分布M.
$\bullet$　判别模型D：用来判别这个不断学习的概率是我们知道的概率分布N还是我们不知道的概率分布M。

https://arxiv.org/abs/1406.2661

模型训练

训练两个模型的方法：单独交替迭代训练
判别模型： 希望真样本集尽可能输出1，假样本集输出0。对于判别网络，此时问题转换成一个有监督的二分类问题，直接送到神经网络模型中训练。
生成网络：目的是生成尽可能逼真的样本。在训练生成网络的时候，需要联合判别网络才能达到训练的目的。

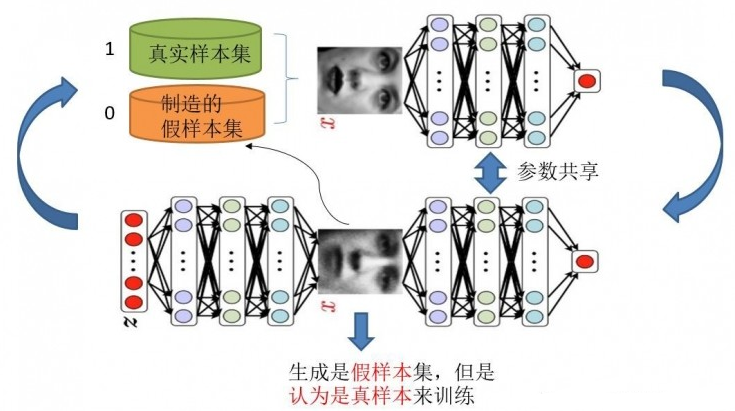
总结：首先固定G，单独训练D，为了让D得到充分训练，有的时候要迭代多次。D训练完毕后，固定D，训练G，如此循环。训练的方式是反向传播算法。

数学推导

符号定义

• $P_{data}(x)$：真实数据的分布

• $P_z(Z)$：噪声数据

• $P_g(x)$：生成模型生成的数据分布

• D(X)：判别器

• G(x)：生成器

定义生成器和判别器

`$E_{x \sim P_{data}}(x) \cdot logD(x)$

由上式可知：当$x \sim P_{data}(x) ,D(x)=1的时，E_{x \sim P_{data}}(x)$取得最大值。

`$E_{x \sim P_{z}}(z) \cdot log(1-D(G(z)))$

由上式可知：当$x \sim P_{z}(z) , D(G(z))=0时，E_{x \sim P_{z}}(z)$取得最大值。

所以为了我们的判别模型越来越好，能力越来越强大，定义目标函数为：

$V(G,D)= logD(x) + log(1-D(G(z)))$

要使判别模型取得最好，所以需要使V(G,D)V(G,D)取得最大，即：

$D = agrmax_DV(G,D)$

当判别模型最好的时候，最好的生成模型就是目标函数取得最小的时候：

$G=argmin_G(aggmax_D(V(G, D)))$

所以经过这一系列的讨论，这个问题就变成了最大最小的问题，即：

`$min_Gmax_DV(G, D)=E_{x \sim P_{data}}(x) \cdot logD(x)+ E_{x \sim P_{z}}(z) \cdot log(1-D(G(z)))$

最优判别模型

最终的目标函数：

`$V(G,D)= \int_x P_{data}(x) \cdot logD(x) + P_g(x)log(1-D(G(z))) d(x)$

令：$V(G,D)=f(y), P_{data}(x)=a, P_g(x)=b$

所以：$f(y)=alogy+blog(1-y)$

因为: $a+b \ne 0$

所以最大值：$\frac{a}{a+b}$

最后，我们得到的最优判别模型就是：

`$D(x)=\frac{P_{data}(X)}{P_{data}(X)+P_g(x)}$

由于生成对抗网络的目的是：得到生成模型可以生成非常逼真的数据，也就是说是和真实数据的分布是一样的。因此最优的判别模型的输出为：

`$D(x)=\frac{P_{data}}{P_{data}+P_g}=\frac12$

其中：$P_g和P_{data}$的数据分布是一样的。

也就是说当D输出为0.5时，说明鉴别模型已经完全分不清真实数据和GAN生成的数据了，此时就是得到了最优生成模型了。

特点

优点：

$\bullet$　模型优化只用到了反向传播，而不需要马尔科夫链。
$\bullet$　训练时不需要对隐变量做推断。
$\bullet$　理论上，只要是可微分函数都能用于构建生成模型G和判别模型D，因而能够与深度神经网络结合–>深度产生式模型。
$\bullet$　生成模型G的参数更新不是直接来自于数据样本，而是使用来自判别模型D的反向传播梯度。

缺点：

$\bullet$　可解释性差，生成模型的分布没有显示的表达。它只是一个黑盒子一样的映射函数：输入是一个随机变量，输出是我们想要的一个数据分布。
$\bullet$　比较难训练，生成模型D和判别模型G之间需要很好的同步。例如，在实际中我们常常需要 D 更新 K次， G 才能更新 1 次，如果没有很好地平衡这两个部件的优化，那么G最后就极大可能会坍缩到一个鞍点。