LSTM

ＬＳＴＭ模型

LSTM（Long Short-Term Memory）是长短期记忆网络，是一种时间递归神经网络，适合于处理和预测时间序列中间隔和延迟相对较长的重要事件。
就是所谓的该记得会一直传递，不该记得就被“忘记”。

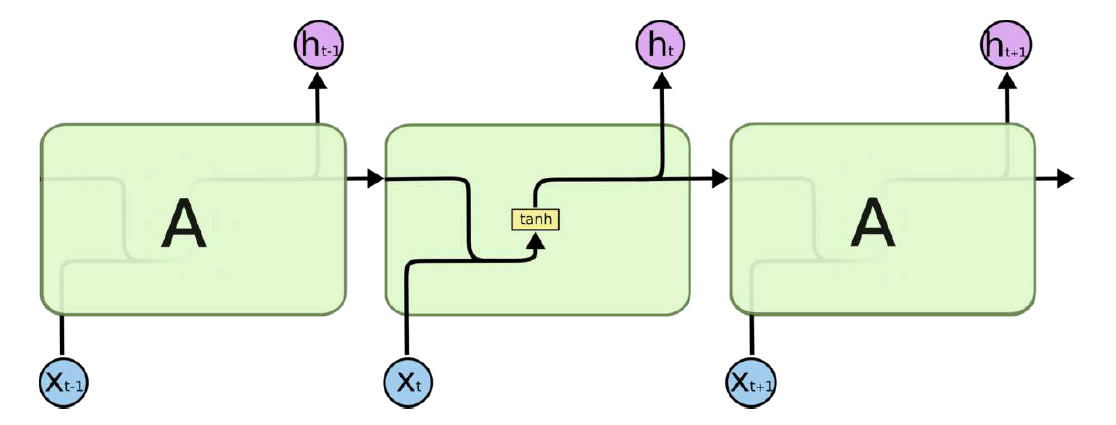
“记忆细胞”变得稍微复杂了一点

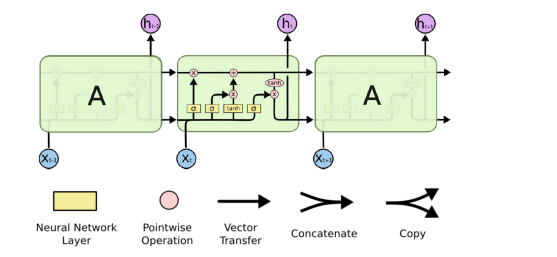
细胞状态

细胞状态类似于传送带。直接在整个链上运行，只有一些少量的线性交互。信息在上面流传会很容易保持不变。

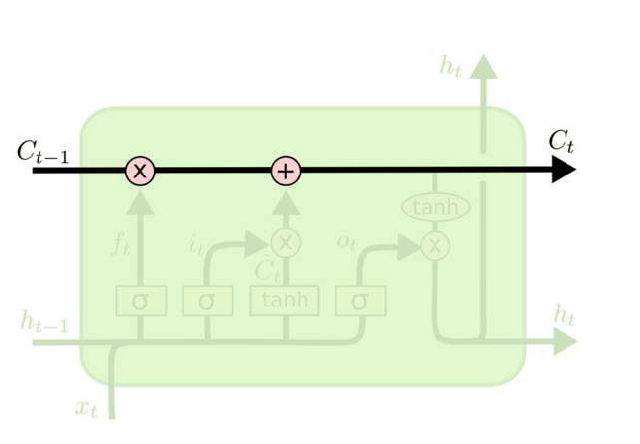
LSTM控制“细胞状态”的方式：

• 通过“门”让信息选择性通过，来去除或者增加信息到细胞状态。
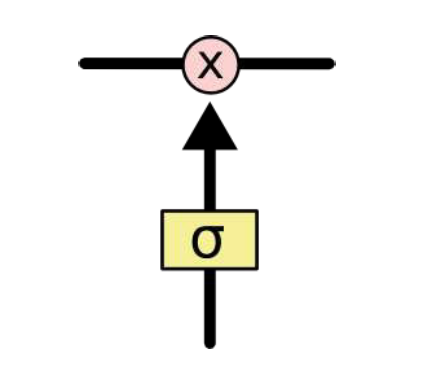
• 包含一个SIGMOD神经元层和一个pointwise乘法操作。
• SIGMOD层输出0到1之间的概率值，描述每个部分有多少量可以通过。0代表“不许任何量通过”，1就表示“允许任意量通过”。

遗忘门

遗忘门（forget gate）顾名思义，是控制是否遗忘的，在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。遗忘门子结构如下图所示：

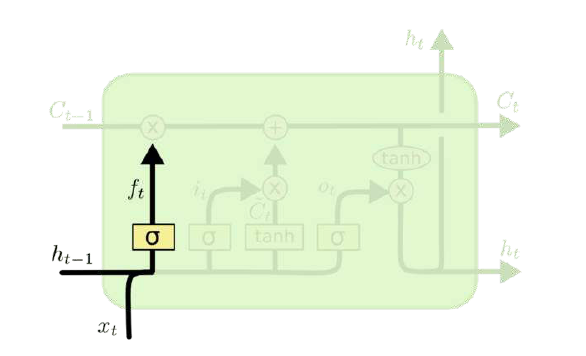
图中输入的有上一序列的隐藏状态$h_{t−1}$和本序列数据$x_t$，通过一个激活函数，一般情况下是SIGMOD，得到遗忘门的输出$f_t$。由于SIGMOD的输出$f_t$在[0,1]之间，因此这里的输出$f_t$代表了遗忘上一层隐藏细胞的概率。

数学表达式：

$$f(t)=\sigma(W_f h_{t-1}+U_f x_t+b_f)$$

其中：$W_f、U_f、b_f$为线性关系的权重项和偏置项，σ为SIGMOD激活函数。

输入门

输入门（input gate）负责处理当前序列位置的输入，它的子结构如下图：

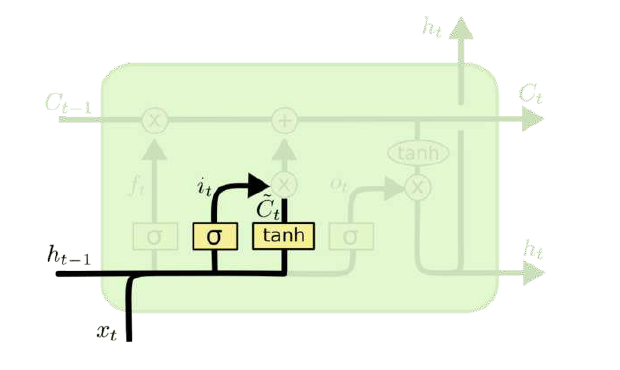
从图中可以看到输入门由两部分组成，第一部分使用了sigmoid激活函数，输出为$i_{(t)}$,第二部分使用了tanh激活函数，输出为$c_{(t)}$, 两者的结果后面会相乘再去更新细胞状态。

• SIGMOD层决定什么值需要更新。
• Tanh层创建一个新的候选值向量$c_{(t)}$
• 第二步还是为状态更新做准备。

数学表达式：

$$i{(t)} = \sigma(W_ih_{t-1} + U_ix_t + b_i)$$ $$\tilde c{(t)} =tanh(W_ah_{t-1} + U_ax_t + b_a)$$

其中$W_i,U_i,b_i,W_a,U_a,b_a$，为线性关系的权重项和偏置项，σ为SIGMOD激活函数。

更新细胞

在研究LSTM输出门之前，我们要先看看LSTM之细胞状态。前面的遗忘门和输入门的结果都会作用于细胞状态 C(t)，我们来看看细胞如何从C(t−1)到C(t):

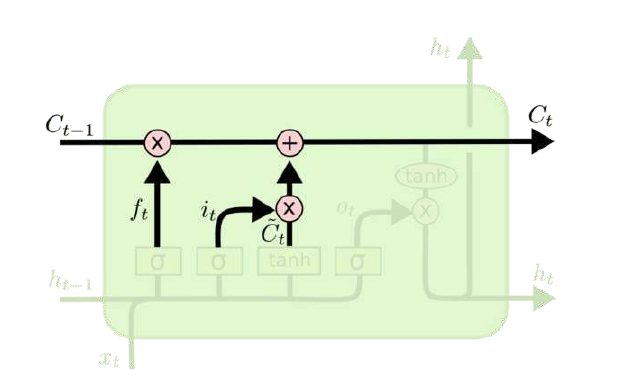
由图可知：细胞状态$C_t$由两部分组成；第一部分是$C_{t−1}$和遗忘门输出$f_t$的乘积，第二部分是输入门的$i_t和\tilde c_{(t)}$的乘积，总结为如下三点：

• 更新$C_{(t−1)}为C_{(t)}$。
• 把$C_{(t−1)}$和$f_{(t)}$相乘，丢弃掉我们确定需要丢弃的信息。
• 加上$i(t) * \tilde c_{(t)}$。最后得到新的候选值，根据我们决定更新每个状态的程度进行变化。

数学表达式：

$$C_{(t)} = C_{(t-1)} \odot f{(t)} + i_{(t)} \odot \tilde c_{(t)}$$

其中，⨀为Hadamard积.

输出门

有了新的隐藏细胞状态C(t)，我们就可以来看输出门了，子结构如下：

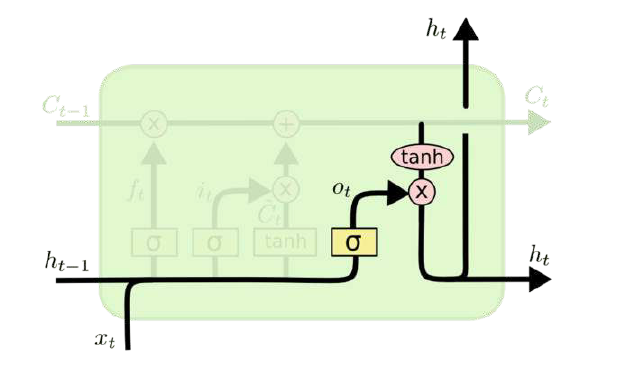
从图中可以看出：隐藏状态$h_t$的更新由两个部分组成：第一部分是$o_t$，它是由上一序列的隐藏状态$h_{t−1}$和本序列的$x_t$，以及激活函数SIGMOD得到的，第二部分是由隐藏状态$C_t和Tanh$激活函数组成，即：

• 最开始先运行一个SIGMOD层来确定细胞状态的哪个部分将输出。
• 接着用tanh处理细胞状态（得到一个-1到1之间的值），再将它和SIGMOD门的输出相乘。输出我们确定输出的那部分值。

数学表达式：

$$o_t=\sigma(W_o[h_{t-1},x_t]+b_o)$$ $$h_t=o_t*tanh(C_t)$$

总结

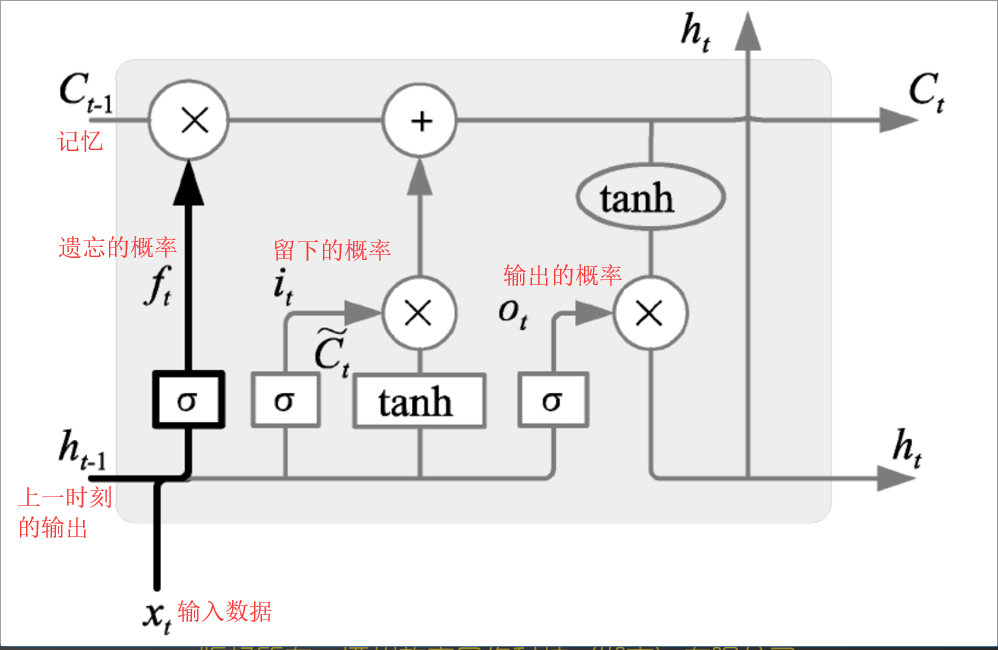
LSTM变体

• 增加peephole connection
• 让门层也会接受细胞状态的输入。

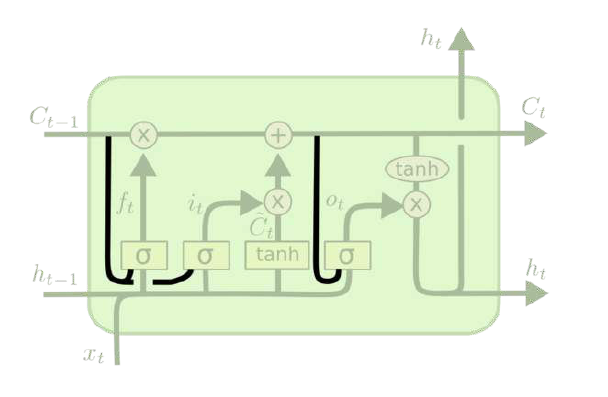
数学表达式：

$$f_t=\sigma(W_f \cdot[C_{t-1}, h_{t-1},x_t]+b_f)$$ $$i_t=\sigma(W_i \cdot[C_{t-1}, h_{t-1},x_t]+b_i)$$ $$o_t=\sigma(W_o \cdot[C_{t-1}, h_{t-1},x_t]+b_o)$$

• 通过使用coupled忘记和输入门
• 之前是分开确定需要忘记和添加的信息，然后一同做出决定。

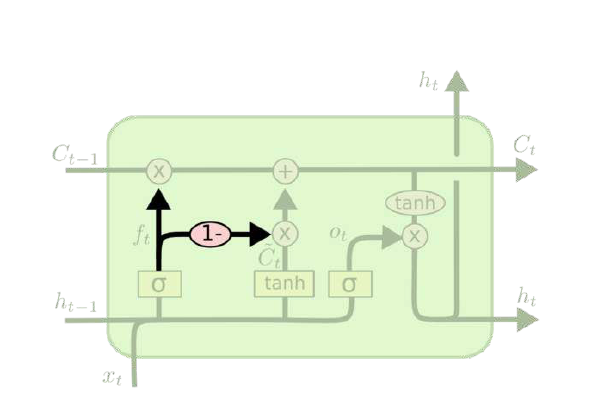
数学表达式：

$$C_t=f_t * C_{t-1}+(1-f_t) * \tilde C_t$$

GRU

Gatad Reacurrent Unit (GRU)，2014年提出。

• 将忘记门和输入门合成了一个单一的更新门
• 混合了细胞状态和隐藏状态
• 比标准的LSTM简单

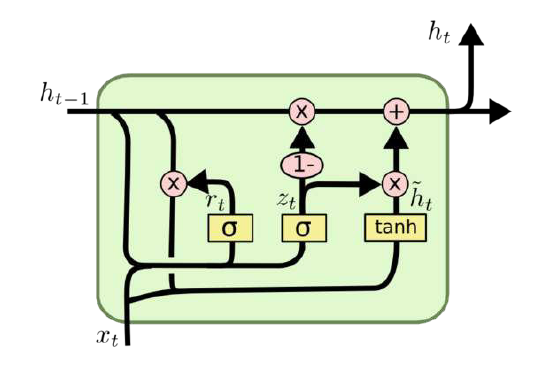
数学表达式：

$$z_t=\sigma(W_z \cdot [h_{t-1},x_t])$$ $$r_t=\sigma(W_r \cdot [h_{t-1},x_t])$$ $$\tilde h_t= tanh(W \cdot [r_t*h_{t-1},x_t])$$ $$h_t=(1-z_t) * h_{t-1} + z_t * \tilde h_t$$

LSTM总结

实现

ＬＳＴＭ

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

# 导入数据
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

# 超参数设置
lr = 0.001  # 学习率
epochs = 100000  # 最大训练次数
batch_size = 128  # 小批量样本数
n_inputs = 28  # Mnist数据输入维度 (img shape: 28*28)
n_steps = 28  # time steps
n_hidden_units = 128  # 隐层神经元
n_classes = 10  # MNIST 分类 (0-9 digits)

# x y placeholder
x = tf.placeholder(tf.float32, [None, n_steps, n_inputs])  # [None, 28, 28]
y = tf.placeholder(tf.float32, [None, n_classes])  # [None,10]

# 对 weights biases 初始值的定义
weights = {
    # shape (28, 128)
    'in': tf.Variable(tf.random_normal([n_inputs, n_hidden_units])),
    # shape (128, 10)
    'out': tf.Variable(tf.random_normal([n_hidden_units, n_classes]))
}
biases = {
    # shape (128, )
    'in': tf.Variable(tf.constant(0.1, shape=[n_hidden_units, ])),
    # shape (10, )
    'out': tf.Variable(tf.constant(0.1, shape=[n_classes, ]))
}


def RNN(X, weights, biases):
    # input layer
    # 原始的 X 是 3 维数据, 我们需要把它变成 2 维数据才能使用 weights 的矩阵乘法
    # X ==> (128 batches * 28 steps, 28 inputs)
    X = tf.reshape(X, [-1, n_inputs])

    # X_in = W*X + b
    X_in = tf.matmul(X, weights['in']) + biases['in']
    # X_in ==> (128 batches, 28 steps, 128 hidden) 换回3维
    X_in = tf.reshape(X_in, [-1, n_steps, n_hidden_units])

    # cell计算
    # 使用 basic LSTM Cell.
    cell = tf.contrib.rnn.BasicLSTMCell(n_hidden_units, forget_bias=1.0, state_is_tuple=True)
    init_state = cell.zero_state(batch_size, dtype=tf.float32)  # 初始化全零 state

    # 使用tf.nn.dynamic_rnn(cell, inputs)，我们要确定inputs的格式。
    # tf.nn.dynamic_rnn中的time_major参数会针对不同inputs格式有不同的值。
    # 如果inputs为（批次，步骤，输入）==> time_major=False;
    # 如果inputs为（步骤，批次，输入）==> time_major=True;
    outputs, final_state = tf.nn.dynamic_rnn(cell, X_in, initial_state=init_state, time_major=False)

    # 输出层

    results = tf.matmul(final_state[1], weights['out']) + biases['out']
    return results


pred = RNN(x, weights, biases)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
train_optimizer = tf.train.AdamOptimizer(lr).minimize(cost)

correct_pred = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

init = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    step = 0
    while step * batch_size < epochs:
        batch_xs, batch_ys = mnist.train.next_batch(batch_size)
        batch_xs = batch_xs.reshape([batch_size, n_steps, n_inputs])
        _ = sess.run([train_optimizer], feed_dict={x: batch_xs, y: batch_ys})
        if step % 20 == 0:
            # 计算批次数据的准确率
            acc = sess.run(accuracy, feed_dict={x: batch_xs, y: batch_ys})
            # Calculate batch loss
            loss = sess.run(cost, feed_dict={x: batch_xs, y: batch_ys})
            print("Iter " + str(step * batch_size) + ", Minibatch Loss= " + \
                  "{:.6f}".format(loss) + ", Training Accuracy= " + \
                  "{:.5f}".format(acc))
        step += 1
    print(" Finished!")
    # 计算准确率 for 128 mnist test images
    test_len = 128
    test_data = mnist.test.images[:test_len].reshape((-1, n_steps, n_inputs))
    test_label = mnist.test.labels[:test_len]
    print("Testing Accuracy:", sess.run(accuracy, feed_dict={x: test_data, y: test_label}))

GRU

import tensorflow as tf
# 导入 MINST 数据集
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("MNIST_data", one_hot=True)

n_input = 28  # MNIST data 输入 (img shape: 28*28)
n_steps = 28  # timesteps
n_hidden = 128  # hidden layer num of features
n_classes = 10  # MNIST 列别 (0-9 ，一共10类)

tf.reset_default_graph()

# tf Graph input
x = tf.placeholder("float", [None, n_steps, n_input])
y = tf.placeholder("float", [None, n_classes])

x1 = tf.unstack(x, n_steps, 1)


# gru
gru = tf.contrib.rnn.GRUCell(n_hidden)
outputs = tf.contrib.rnn.static_rnn(gru, x1, dtype=tf.float32)

pred = tf.contrib.layers.fully_connected(outputs[-1], n_classes, activation_fn=None)

learning_rate = 0.001
training_iters = 100000
batch_size = 128
display_step = 10

# Define loss and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)

# Evaluate model
correct_pred = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

# 启动session
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    step = 1
    # Keep training until reach max iterations
    while step * batch_size < training_iters:
        batch_x, batch_y = mnist.train.next_batch(batch_size)
        # Reshape data to get 28 seq of 28 elements
        batch_x = batch_x.reshape((batch_size, n_steps, n_input))
        # Run optimization op (backprop)
        sess.run(optimizer, feed_dict={x: batch_x, y: batch_y})
        if step % display_step == 0:
            # 计算批次数据的准确率
            acc = sess.run(accuracy, feed_dict={x: batch_x, y: batch_y})
            # Calculate batch loss
            loss = sess.run(cost, feed_dict={x: batch_x, y: batch_y})
            print("Iter " + str(step * batch_size) + ", Minibatch Loss= " + \
                  "{:.6f}".format(loss) + ", Training Accuracy= " + \
                  "{:.5f}".format(acc))
        step += 1
    print(" Finished!")

    # 计算准确率 for 128 mnist test images
    test_len = 128
    test_data = mnist.test.images[:test_len].reshape((-1, n_steps, n_input))
    test_label = mnist.test.labels[:test_len]
    print("Testing Accuracy:", sess.run(accuracy, feed_dict={x: test_data, y: test_label}))