背景

最大间隔分类器
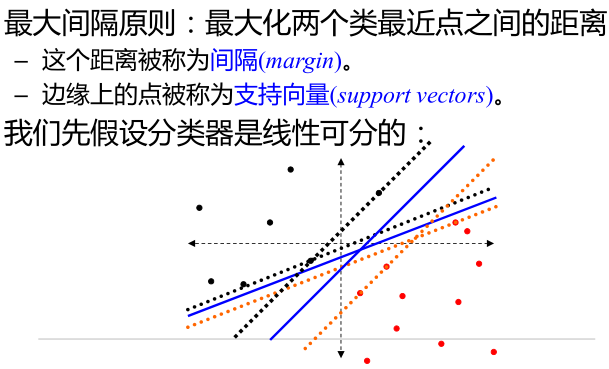
距离的计算
在样本空间中,划分超平面可通过如下线性方程描述:
样本空间中任意点x到超平面的距离可写为:
数据标签定义

优化的目标

目标函数


拉格朗日乘子法

SVM求解
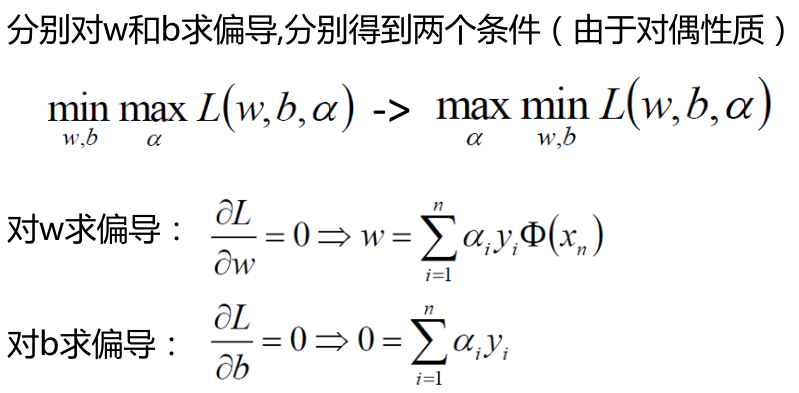

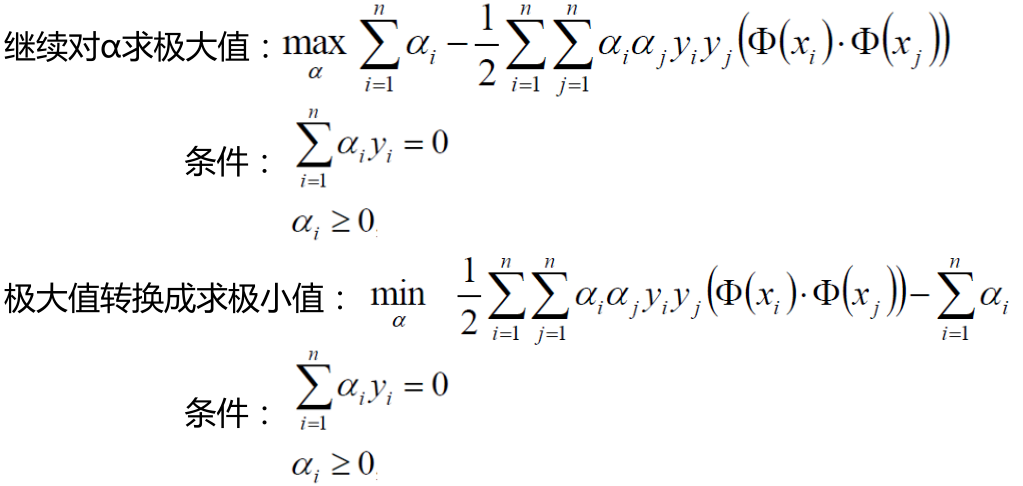
SVM求解实例
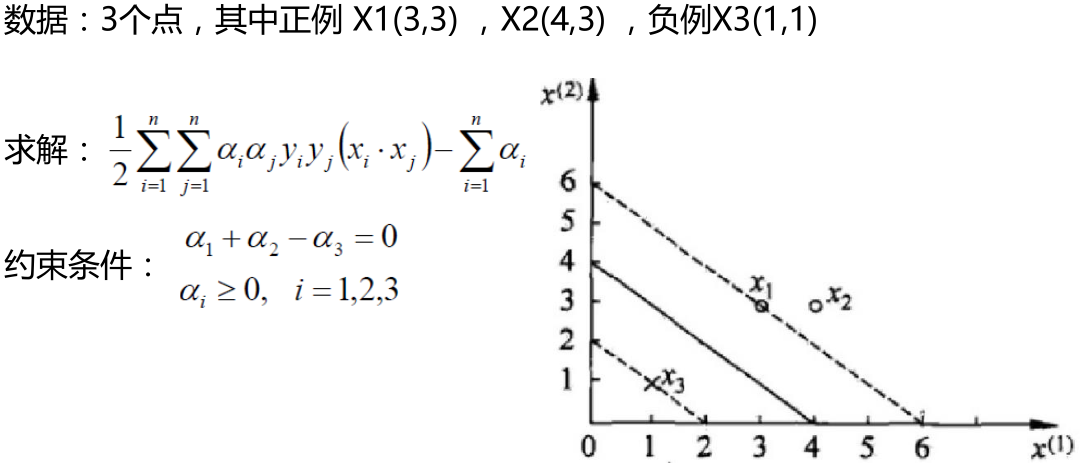


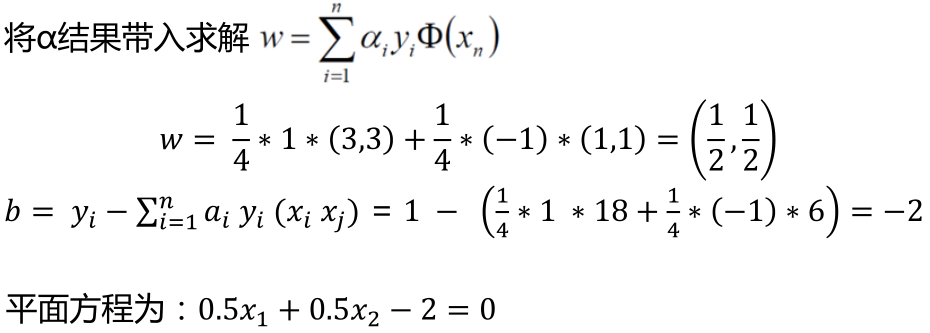
支持向量:真正发挥作用的数据点,ɑ值不为0的点
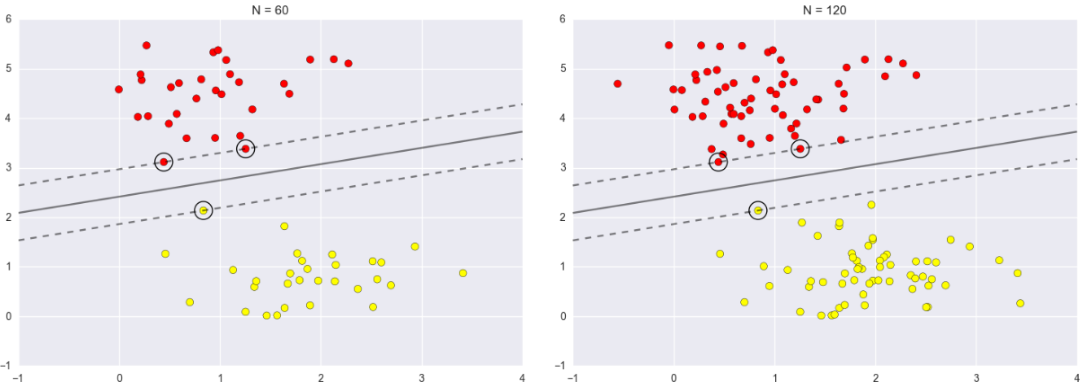
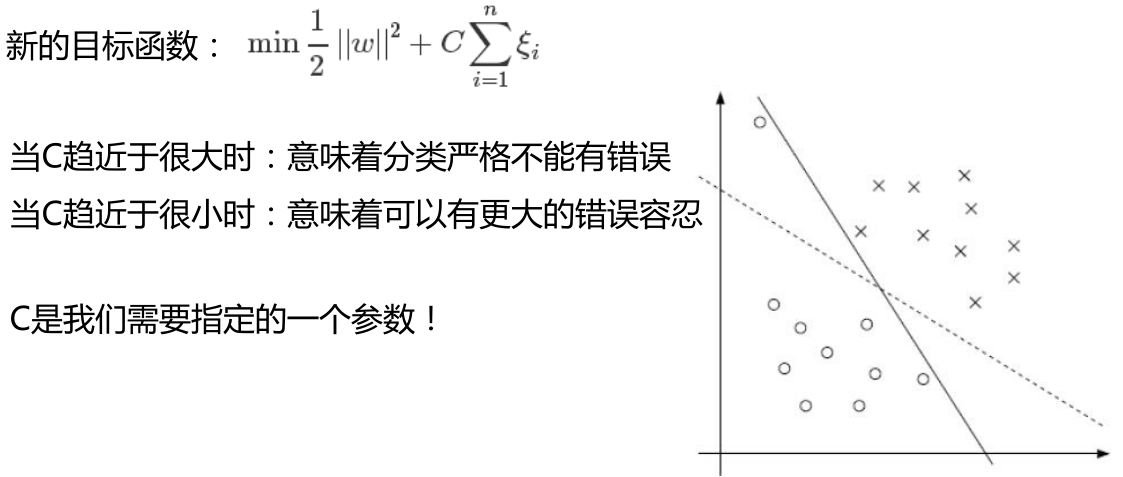
带松弛因子的SVM:C-SVM
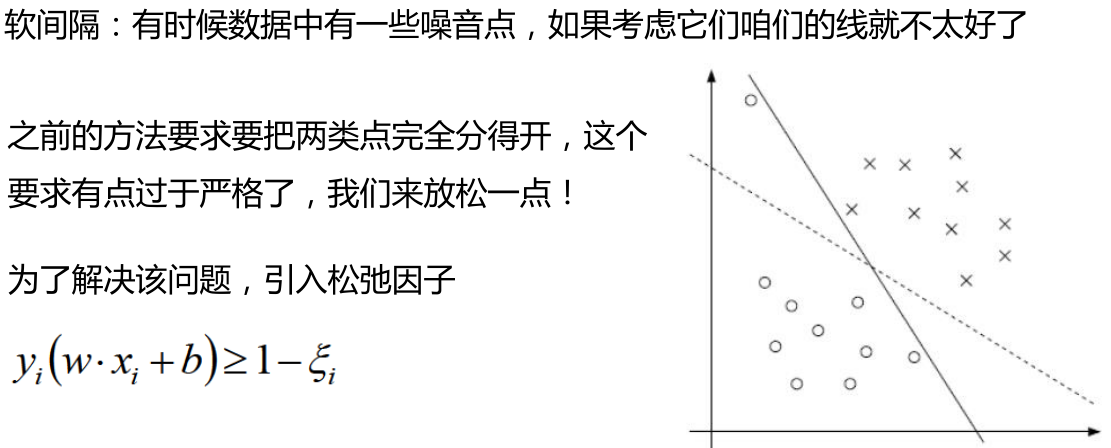
soft-margin

核方法

低维不可分问题
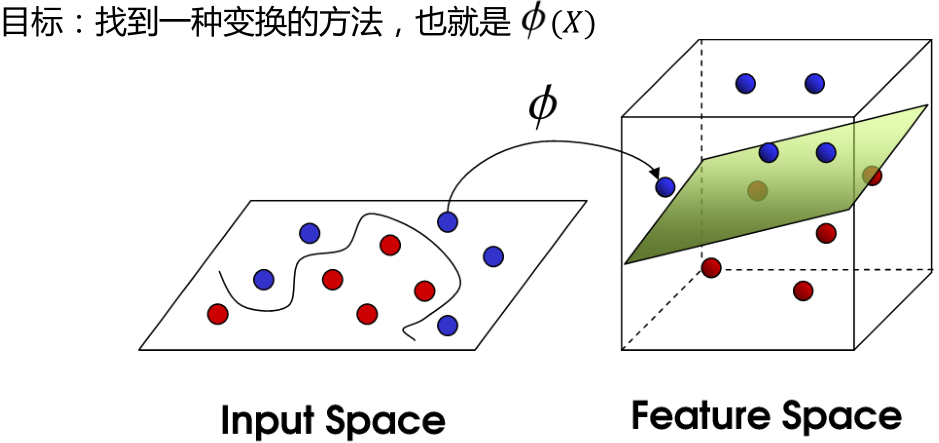

常用核函数

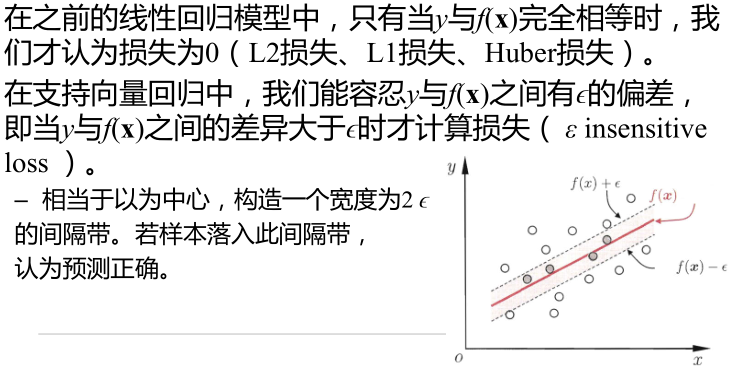
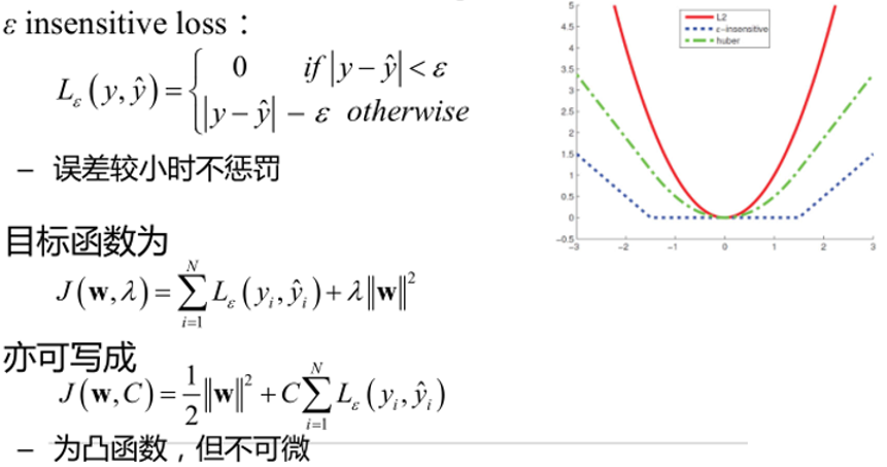
支持向量回归(SVR)


Scikit learn 中的SVM实现

Scikit learn 中的SVC实现

核函数kernel

RBF核的参数

RBF核—核参数正好
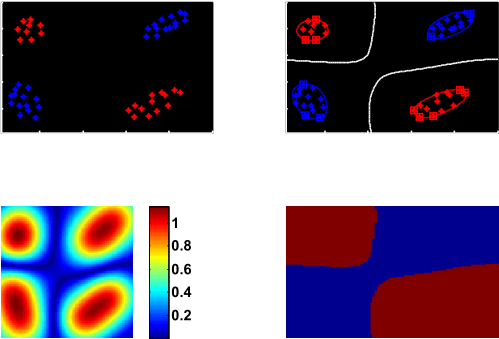
RBF核—欠拟合
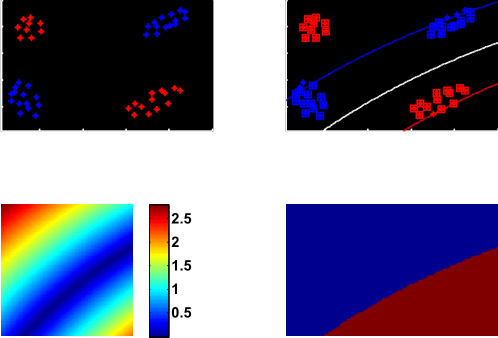
RBF核—过拟合
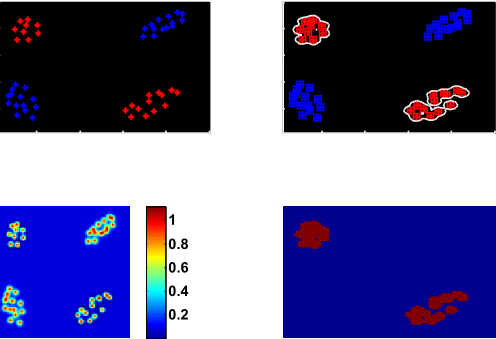
总结
SVM的优点:
– 在高维空间中行之有效
– 当维数大于样本数时仍然可用(但性能不好)
– 在决策函数中只使用训练点的一个子集(支持向量),大大节省了内存开 销
– 用途广泛:决策函数中可使用不同的核函数
• 劣势:
– SVM不直接提供概率估计
– 可通过交叉验证计算,代价比较高
• Scikit-learn中的支持向量机同时支持密集样本向量(numpy.ndarray和可通过numpy.asarray转化的数据类型)和稀疏样本向量(任何scipy.sparse对象)。但如果想用SVM对稀疏数据进行预测,则必须先在这些数据上拟合。为了优化性能,应该使用C阶(C-Ordered)numpy.ndarray(密集的)或scipy.sparse.csr_matrix(稀疏的),并指定dtype=float64